Conversion Analogique - Numérique et Numérique - Analogique

Introduction

L'ESP32 possède deux convertisseurs analogique - numérique (Analog to Digital converter, ADC) 16 bits du type SAR (Successive Approximation Register) et deux convertisseurs numérique - analogique (Digital to Analog Converter, DAC) de 8 bits. Cherchant des pilotes dans le manuel Micropython je trouve seulement la description de l'ADC. Dans le code source de MicroPython par contre je vois qu’aussi le pilote pour le DAC est disponible.

L'ADC

ADC2 est utilisé pour le WiFi et pour cette raison n'est pas accessible à nous. L'ADC 1 par contre possède une entrée multiplexée et huit canaux sont utilisables (sur les pins 32-39). L'ADC travaille dans un intervalle de 0..1V mais ils existent des atténuateurs pour étendre cette gamme. Une atténuation de 11 dB résulte dans une gamme approximative 0..3.6V.

Le DAC

Les DAC sont accessibles sur les pins 25 et 26. Puisqu’il n'y a pas de descriptions dans le manuel MicroPython, voila un exemple d'accès au DAC :

rom machine import Pin,DAC
from time import sleep_ms

dac = DAC(Pin(26))
print("Running a triangular wave form with a frequency of ~ 1 Hz on pin 26")
while True:
    for i in range(256):
        dac.write(i)
        sleep_ms(2)
    for i in range(256):
        dac.write(256-i-1)
        sleep_ms(2)

Ceci produira une onde triangulaire lente, qu'on peut observer avec un multimètre.

Vérification de la linéarité

Si on connecte le DAC avec l'entrée d'un ADC et on monte la valeur envoyée au DAC linéairement de zéro au maximum de 255 on s'attend à une courbe de valeurs lus de l'ADC parfaitement linéaire. Ceci est vrai si aussi bien le DAC que L'ADC sont linéaire.

Courbe de linéarité attendu	Courbe de linéarité mesuré

Comme on voit, la courve devient très non-linéaire pour des valeurs dépassant les valeurs DAC de 255 (3.3V * 200 / 256: ~ 2.6 V). Malheureusement nous de savont pas si l'ADC ou le DAC est responsable pour cette non-linéarité. On voit aussi que la courbe ne passe pas par 0,0 comme on pourrait s'attendre.

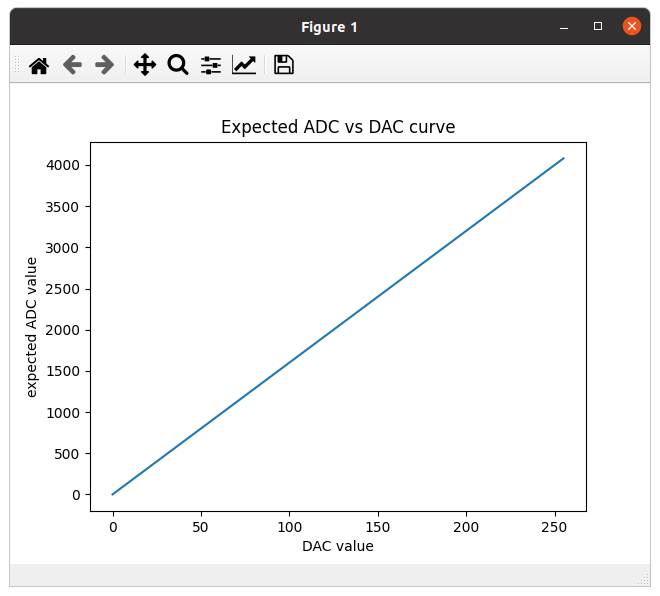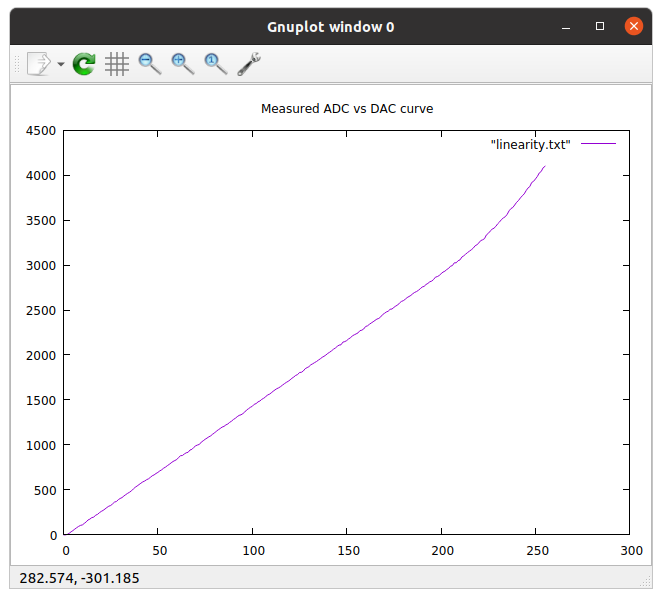Vérification de linéarité avec un ADC ADS1115 externe

L'ADS1115 est un ADC haute précision de 16 bit du type Signa/Delta avec une interface I2C. On peut facilement le connecté sur les pins I2C SCL et SDA de la carte CPU. Les connexions pour la CPU WeMos D1 mini sont spécifie dans le tableau ci-dessous:

ADS 1115	WeMos D1 bus and ESP32	WeMos D1 bus and ESP8266
Vdd	3.3V	3.3V
Gnd	Gnd	Gnd
SCL	D1: GPIO 22	D1: GPIO 5
SDA	D2: GPIO 21	D2: GPIO 4
A0	DAC 2: GPIO 26

Un pilote existe pour l'ADS1115 facilitant le teste : https://github.com/robert-hh/ads1x15.

J'ai copié le pilote dans /lib de l'ESP32 avec ampy et j'ai modifié mon programme ADC vs DAC en utilisant l'ADS1115 au lieu de l'ADC de l'ESP32. Voilà le résultat :

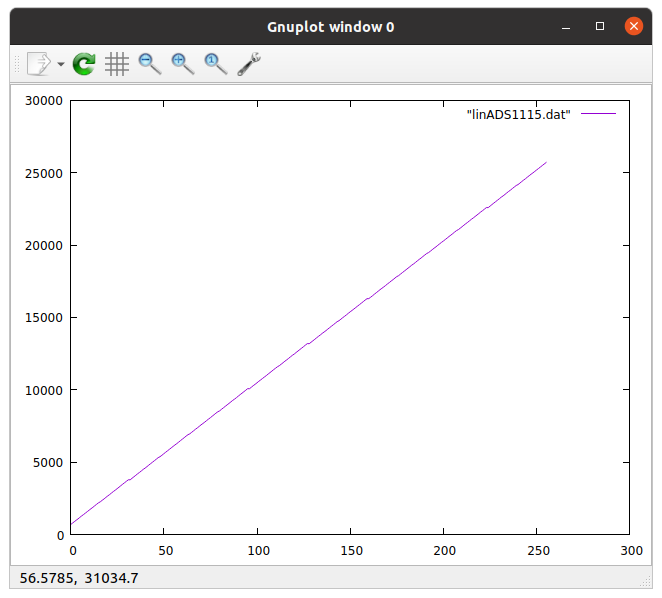Notez le changement d'échelle sur l'axe y. L'ADS1115 est un ADC 16 bit tandis que l'ADC de l'ESP32 utilise 12 bits seulement. Le maximum sur l'axe y dépend de la gamme de tension d'entrée sélectionnée. Ceci démontre clairement que c'est ADC de l'ESP32 est le coupable.

Correction de la non-linéarité par software

Puisque nous savons maintenant que le DAC est bien linéaire et que c'est l'ADC qui introduit la non-linéarité nous pouvons utiliser notre première mesure DAC vs ADC comme courbe de calibration. Si nous pouvons calculer la valeur DAC à partir d'une valeur ADC nous pouvons aussi corriger la non-linéarité.

Pour accomplir ceci nous devons d'abord invertir (replacer les valeurs x par les valeurs y et vice vers) la fonction adc = y = f(x) ou x est la valeur du DAC. Ceci est la fonction du premier graphe (noir, partiellement couvert par le graphe rouge). En suite, nous pouvons calculer une approximation polynomiale à la fonction invertie (graphe rouge).

Le polynôme du grade 5 est défini comme suit :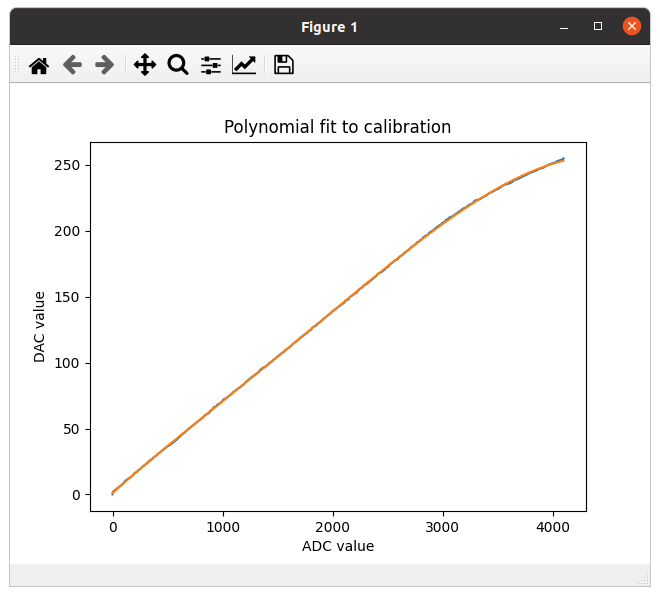

La fonction polyfit du module Python numpy est utilisé pour calculer cette approximation et elle retourne les coefficients a..f du polynôme. Le polynôme ainsi obtenu est utilisé pour calculer la valeur d'entrée corrigée. Au lieu de retourner la valeur lu de 'ADC nous entrons cette valeur dans le polynôme et nous retournons la valeur calculée, multiplier par 16 pour adapter la gamme 0..225 a la gamme de l'ADC: 0..4095.

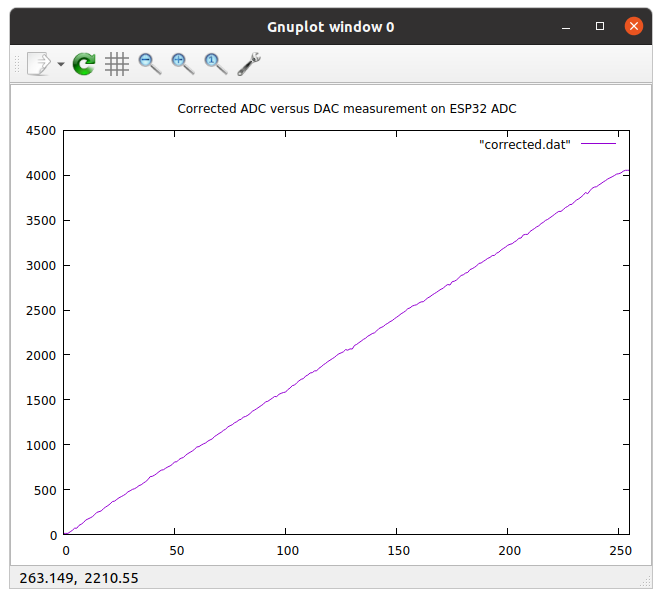
Voilà le graphe ADC vs DAC corrigé avec le polynôme de calibration.

-- Uli Raich - 2021-07-04

Comments